Contents
Abstract. Due to the existence of a) gauge fields and b) fermion fields, the geometry of physics is higher supergeometry, i.e. super-geometric homotopy theory. This is made precise via Grothendieck‘s functorial geometry implemented in higher topos theory. We give an introduction to the higher topos of higher superspaces and how it accomodates higher Lie theory of super L-∞ algebras. We close by indicating how geometric homotopy theory reveals that the superpoint emerges “from nothing”, and that core structure of M-theory emerges out of the superpoint via a sequence of invariant universal higher central extensions. This will be discussed in more detail in other talks in the meeting, notably in
all summed up in the proceedings contribution:
Contents
Motivation
The geometry of fundamental physics is higher differential supergeometry.
Here:
-
Supergeometry is geometry whose spaces may have algebras of functions that are -graded-commutative algebras. This is the mathematical reflection of the Pauli exclusion principle, which says that a fermionic wave function on a phase space of a physical system with fermions has to have vanishing square. By linearity this implies that
and hence that fermionic wave functions anti-commute, and hence are the odd-graded elements in a commutative superalgebra (a slightly noncommutative algebra!)
Ever since the existence of fermionic particles was experimentally established, around the time of the Stern-Gerlach experiment in the 1920s, it is thus an experimental fact that fundamental physics is described by supergeometry. (This is not necessarily super-symmetric, though of course there is a close relation.)
-
Higher structures is short for higher homotopy theoretic structures and reflects the gauge principle of physics: This says that, generally, it does not make invariant sense to ask if any two things , (e.g. field histories) are equal, instead one must ask for a gauge transformation between them, mathematically a homotopy:
This principle applies also to gauge transformations themselves, and thus leads to gauge-of-gauge transformations
and so on to ever higher gauge transformations:
mathematically reflected by higher homotopies in higher homotopy types.
Ever since the existence of gauge fields was understood in the 1920s, it is thus an experimental fact that fundamental physics is described by higher geometry.
A striking consequence is that, both in higher geometry as well as in supergeometry and therefore in the geometry of fundamental physics, spaces generally are not sets of points, as in the traditional definition of topological spaces or differentiable manifolds.
What, then, is the geometry of fundamental physics?
The right framework to answer questions like this has been urged by Alexander Grothendieck already in Grothendieck 73 (see Lawvere 03) and has been much expanded on by William Lawvere (e.g. Lawvere 97, Lawvere 91) and has an evident lift to higher geometry (Lurie 09, S. 13), but has remained somewhat of a “public secret”:
The answer is known, alternatively, as (higher) functorial geometry (Grothendieck) or synthetic differential geometry in gros toposes (Lawvere), or variants thereof.
In this lecture series we try to give a quick but self-contained introduction to higher differential supergeometry this way, following Schreiber 13.
We begin at the beginning, with introducing relevant basics of category theory, topos theory and homotopy theory. As a running example, we incrementally construct the higher topos of higher supergeometry. Along the way we provide pointers to applications in perturbative quantum field theory and the theory of fundamental super p-branes.
In view of M-theory we close by briefly highlighting the following phenomena, which are being expanded on in other talks at the meeting.
See also the exposition at:
Super p-Brane Theory emerging from Super Homotopy Theory
talk at String Math 2017, Hamburg (slides, expo, video)
1) category theory is really the theory of duality, formalized in the guise of adjunctions, hence adjoint pairs, and more generally adjoint triples for “dualities of dualities” (Lawvere 69, Lambek 82).
Moreover, this does capture duality in string theory.
Notably double dimensional reduction of fundamental super p-branes is given by the right base change adjunction along the point inclusion into the moduli stack of torus-principal bundles. This fact gives rise to:
2) supergeometry is stratified by a system of adjoint modalities ("super-differential cohesion") that progresses from the initial object to homotopy localization at the superpoint .
Such an abstract characterization of higher supergeometry provides a powerful means to reason about complicated phenomena such as torsion-free G-structures on supergeometric orbifolds by means of modal homotopy type theory (Wellen 18).
This is necessary for studying global properties of black M-branes at ADE-singularities (Huerta-Sati-S. 18, see also the talk by H. Sati (here) at the meeting).
3) out of the superpoint emerges spacetime and the brane bouquet, by regarding the superpoint as a super L-∞ algebra and then applying the microscope of homotopy theory – the Postnikov-Whitehead tower (Fiorenza-Sati-S. 13, Huerta-S. 17, see the talks by J. Huerta (here) and H. Sati (here) at the meeting):
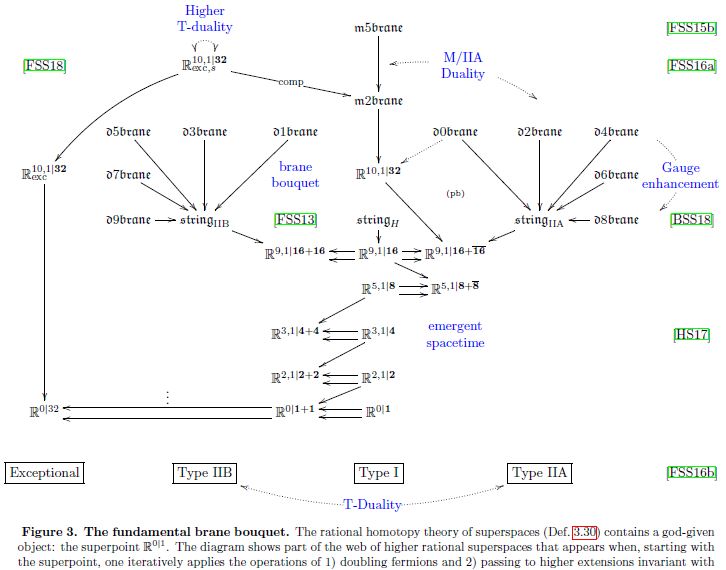
(graphics taken from Huerta-Sati-S. 18)
Lecture notes
Details behind the topics of the talk are in these two chapters from the lecture notes geometry of physics:
-
categories and toposes
-
supergeometry
For further lecture notes on applications see these two chapters:
-
perturbative quantum field theory
-
fundamental super p-branes.
Slides
click here to vertically adjust
then use ‘page down’ from here on
Abstract. Due to the existence of a) gauge fields and b) fermion fields, the geometry of physics is higher supergeometry, i.e. super-geometric homotopy theory. This is made precise via Grothendieck‘s functorial geometry implemented in higher topos theory. We give an introduction to the higher topos of higher superspaces and how it accomodates higher Lie theory of super L-∞ algebras. We close by indicating how geometric homotopy theory reveals that the superpoint emerges “from nothing”, and that core structure of M-theory emerges out of the superpoint, as will be discussed in more detail in other talks in the meeting.
1) Duality theory
We are concerned with duality.
Informally:
Two complementary perspectives whose unity reveals deeper reality.
For instance:
-
in the theory of everything of 19th century philosophy:
duality of opposites in the Science of Logic;
-
in the theory of everything of 20th and 21st century physics:
duality in string theory.
Public secret:
Mathematical formalization of duality is
adjunction, adjoint equivalence, adjoint modality
The theory of duality/adjunction is category theory.
(Lambek 82, Lawvere 69).
A category of objects is
a set (or class) of elements,
but remembering how these may be mapped to each other,
the (homo-)morphisms between them
structuralism:
nature of objects in a category
is reflected in their sets of morphisms to all other objects.
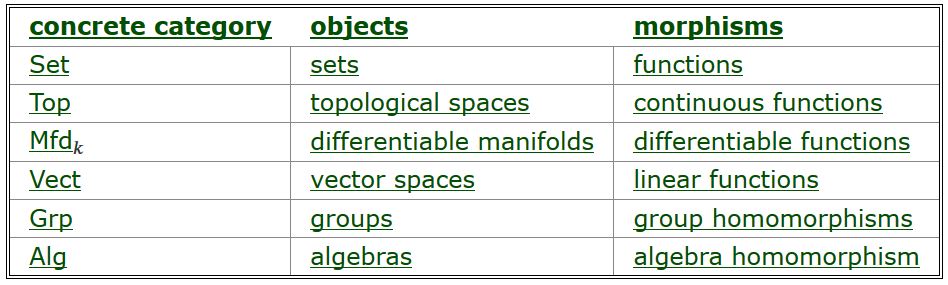
Examples of concrete categories
A functor between two categories
is a function between their objects and morphisms
which preserves the composition of morphisms.
Example. Adding a compact dimension is
an endofunctor on the category of topological spaces
This means that if
is a p-brane worldvolume in , then
is the corresponding (p+1)-brane worldvolume in
which wraps the compact fiber space.
Example – Forming free loop spaces is
an endofunctor on the category of topological spaces
This means that if
is a map of target spaces
for instance a KK-compactification-projection, then
is the corresponding map of closed string configuration spaces
A natural transformation
is an indexed set of morphisms between images of functors
that respects composition on both sides.
Example. – Brane wrapping circle fiber
Every topological space maps into
the free loop space of its Cartesian product with the circle
by sending each point to the loop which wraps the compact fiber space above it.
Conversely, there is the evaluation map
These are natural transformations
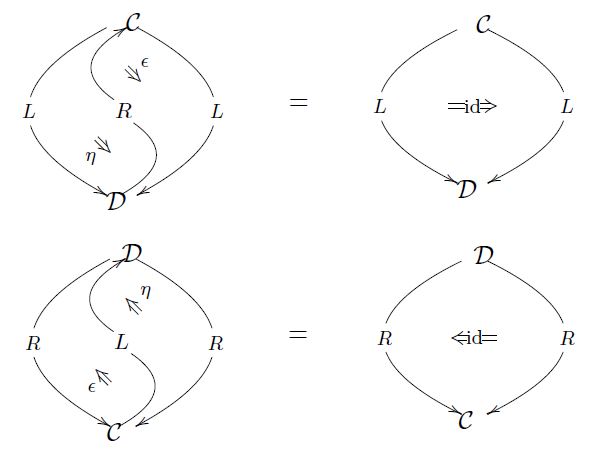
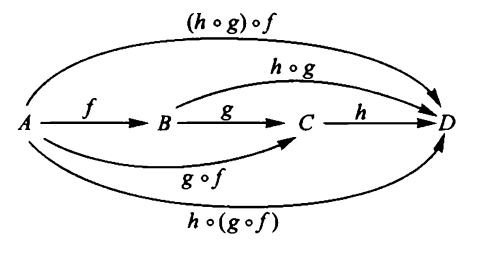
An adjunction of categories
is a pair of functors back and forth
equipped with
natural transformations
satisfying “zig-zag identity”
as shown on the right.
This is equivalent to
hom-set natural bijection:
Example - Cartesian product/mapping space adjunction
The adjunct of a wrapped brane worldvolume
is the double dimensional reduction
From this follows (more here )
-
duality between M-theory and type IIA string theory
-
T-duality between type IIA and IIB string theory
on brane charges in rational super homotopy theory (Fiorenza-Sati-S. 16, BraunackMayer-Sati-S. 18).
see the talks by D. Fiorenza (here) and by V. Braunack-Mayer (here) at the meeting.
Example – Functors assigning algebras of functions
Given any kind of space and a coefficient space
there is a functor which
-
sends spaces to their algebras of functions;
-
sends maps between spaces to the precomposition with these maps:
on the right the opposite category of algebras:
direction of morphisms reversed.
In good cases this is a fully faithful functor
meaning that there is a natural bijection
from sets of morphisms on the left to those on the right:
By the “structuralism” of category theory,
this means that such spaces
may just as well be regarded in the dual algebraic picture.
A fully faithful functor becomes an equivalence of categories
after corestriction to its essential image
duality between geometry and algebra:
archetypical example: Gelfand duality:
More Examples of Isbell duality between geometry and algebra
| geometry | category | dual category | algebra |
|---|
| topology | | | commutative algebra |
| topology | | | comm. C*-algebra |
| noncomm. topology | | | general C*-algebra |
| algebraic geometry | | | fin. gen.
commutative algebra |
noncomm. algebraic
geometry | | | fin. gen.
associative algebra |
| differential geometry | | | commutative algebra |
| supergeometry | | | supercommutative
superalgebra |
formal higher
supergeometry
(super Lie theory) | | | differential graded-commutative
superalgebra
(“FDAs”) |
2) Superalgebra
A differential graded-commutative superalgebra
is a -graded algebra
equipped with a derivation differential of degree .
with either of these sign rules:

Special cases of dgc-superalgebras
Example – The Grassmann algebra (Grassmann 1844)
is the free supercommutative superalgebra over
on odd-graded generators:
Example – A super Cartesian space
is the formal dual space of the tensor product of algebras
differential forms on super Cartesian space
is the differential graded-commutative superalgebra
free over
on
-
generators in bi-degree
-
generators in bi-degree
hence
Bi-Degrees and signs for super differential forms
| generator | bi-degree |
|---|
| (0,even) |
| (0,odd) |
| (1,even) |
| (1,odd) |
| sign rule | Deligne’s | Bernstein’s |
|---|
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
pullback of super differential forms
Each morphism
has unique dg-extension
This defines another fully faithful functor
For a super Lie algebra of finite dimension,
its Chevalley-Eilenberg algebra
is the differential graded-commutative superalgebra
equipped with the differential
which is the linear dual of the super Lie bracket
Equivalently:
is the dgc-superalgebra of left-invariant super differential forms
on the corresponding simply connected super Lie group.
key Example – super Minkowski spacetime
For
and a real spin representation of
the super-translation supersymmetry super Lie algebra
has Chevalley-Eilenberg algebra generated by
with differential
If we think of super Minkowski spacetime
as the super Cartesian space with coordinates
then these generators correspond to
the super-left invariant
super vielbein
Homomorphisms of super Lie algebras
are in natural bijection with
the dual homomorphisms of dgc-superalgebras
between their Chevalley-Eilenberg algebra,
hence we have another fully faithful functor
Hence: A super L-∞ algebra of finite type is
-
a -graded super vector space
degreewise of finite dimension
-
for all a multilinear map
of degree
such that the graded derivation
squares to zero:
This defines a dgc-superalgebra
super L-∞ algebras form the full subcategory
Side remarks.
-
We may drop the assumption of degreewise finiteness
by regarding as
a free graded co-commutative coalgebra
and as a differential
making a differential graded coalgebra.
-
The above definition is for non-curved L-∞ algebras
but allows for “curved sh-maps”.
This is important in the discussion of Super topological T-Duality.
(see the talk by D. Fiorenza at the meeting)
-
By allowing algebras of smooth functions in degree 0
we obtain super-L-∞ algebroids (Sati-S.-Stasheff 12, A.1)
formally dual to super dg-manifolds.
convoluted History:
-algebras were explicitly introduced in Lada-Stasheff 92
but following their discovery by Zwiebach 89, Zwiebach 92 in closed string field theory.
The equivalence to Chevalley-Eilenberg dg-(co-)algebras
is due to Lada-Markl 94, see Sati-Schreiber-Stasheff 08, around def. 13.
But these dual CE-algebras of super L-∞ algebras of finite type
were introduced already in van Nieuwenhuizen 82, D’Auria-Fré 82
for higher super Cartan geometry of supergravity, there called FDAs.
The string theory-community began to pay attention with Hohm-Zwiebach 17
Higher Lie algebras turn out to be the answer to the question:
What do higher Lie algebra cocycles classify?
Recall:
A (p+2)-cocycle on a Lie algebra is
-
multi-linear, skew-symmetric function ;
-
cocycle condition: for all -tuples in
In terms of Chevalley-Eilenberg algebras this means simply
-
-
(this is the classical use of CE-algebras)
A Lie algebra 2-cocycle
corresponds to a central Lie algebra extension,
the new Jacobi identity is the cocycle condition on .
In terms of dual Chevalley-Eilenberg algebras this means simply:
the new nilpotency is the cocycle condition on
Non-classical Fact:
A -cocycle still corresponds to
a higher central extension to an L-∞ algebra
In terms of dual Chevalley-Eilenberg algebras this means simply
Example – string Lie 2-algebra
Every semisimple Lie algebra carries a Killing form pairing
and the resulting trilinear map
is a 3-cocycle.
This classifies a Lie 2-algebra extension of ,
called the string Lie 2-algebra
(Baez-Crans 03, Baez-Crans-S.-Stevenson 05).
In string theory/M-theory this controls
Generally: For a super L-∞ algebra
-
an -cocycle is ,
-
the higher central extension it classifies has
Hence from any super L-∞ algebra emanates a “bouquet” of consecutive higher central extension
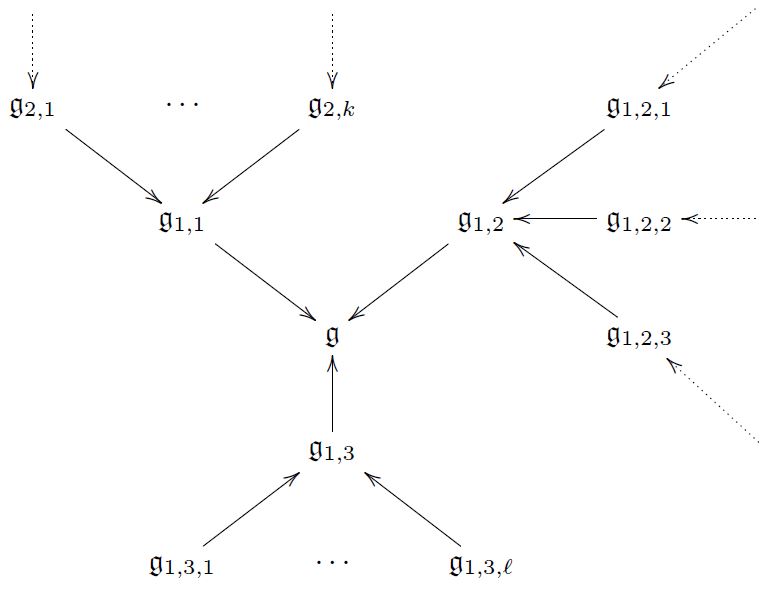
3) Homotopy theory
Traditionally, mathematics and physics
have been founded on set theory,
whose concept of sets is that of “bags of distinguishable points”.
But fundamental physics is governed by the gauge principle.
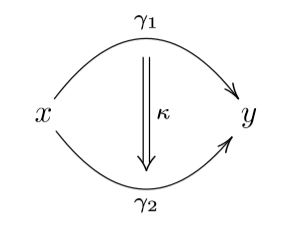
This says that given any two “things”,
such as two field histories and ,
it is in general wrong to ask whether they are equal or not,
instead one has to ask where there is a gauge transformation
between them.
In mathematics this is called a homotopy.
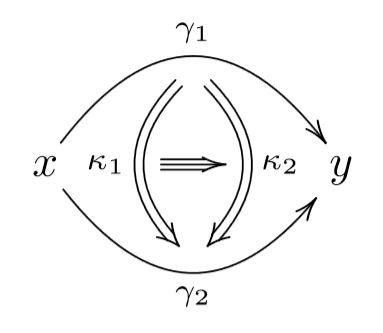
The gauge principle applies to gauge transformations/homotopies themselves,
and thus leads to gauge-of-gauge transformations or homotopies of homotopies

and so on to ever higher gauge transformations or higher homotopies:

A collection of elements with higher gauge transformations/higher homotopies
is called a higher homotopy type.
Hence the theory of homotopy types
– homotopy theory –
is much like set theory,
but with the concept of gauge transformation
built right into its foundations.
Homotopy theory is gauged mathematics.
A model for homotopy
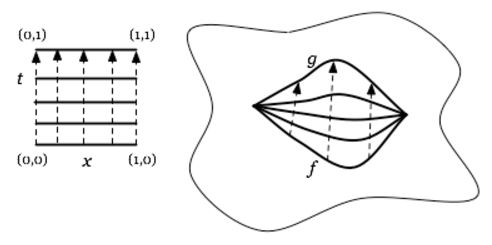
may be given by
| left homotopy | right homotopy |
|---|
| |
A category with a good supply of
-
cylinder objects
-
path space objects
allowing homotopy theory this way
is called a model category
short for “category of models for homotopy types”.
Induced: Its homotopy category whose
-
objects are good models for homotopy types;
-
morphisms are homotopy classes of morphisms in
Example – topological homotopy theory
The category Top of topological spaces
becomes a model category, Top
via the usual cylinder spaces and path spaces
Example – dgc-algebraic super homotopy theory
The category of real differential graded-commutative superalgebras
carries a “projective” model category structure
with path space objects given by tensor product of algebras with
(Bousfield-Gugenheim 76, Carchedi-Roytenberg 12)
Example – simplicial homotopy theory
An n-simplex is an -dimension generalization of a triangle.
A simplicial complex is a space glued from simplices of any dimension.
Generally, a simplicial set is
for each a set of would-be -simplices,
and functions between these sets that behave like
-
sending -simplices to their -dimensional faces,
-
constructing degenerate -simplices on given -simplices.
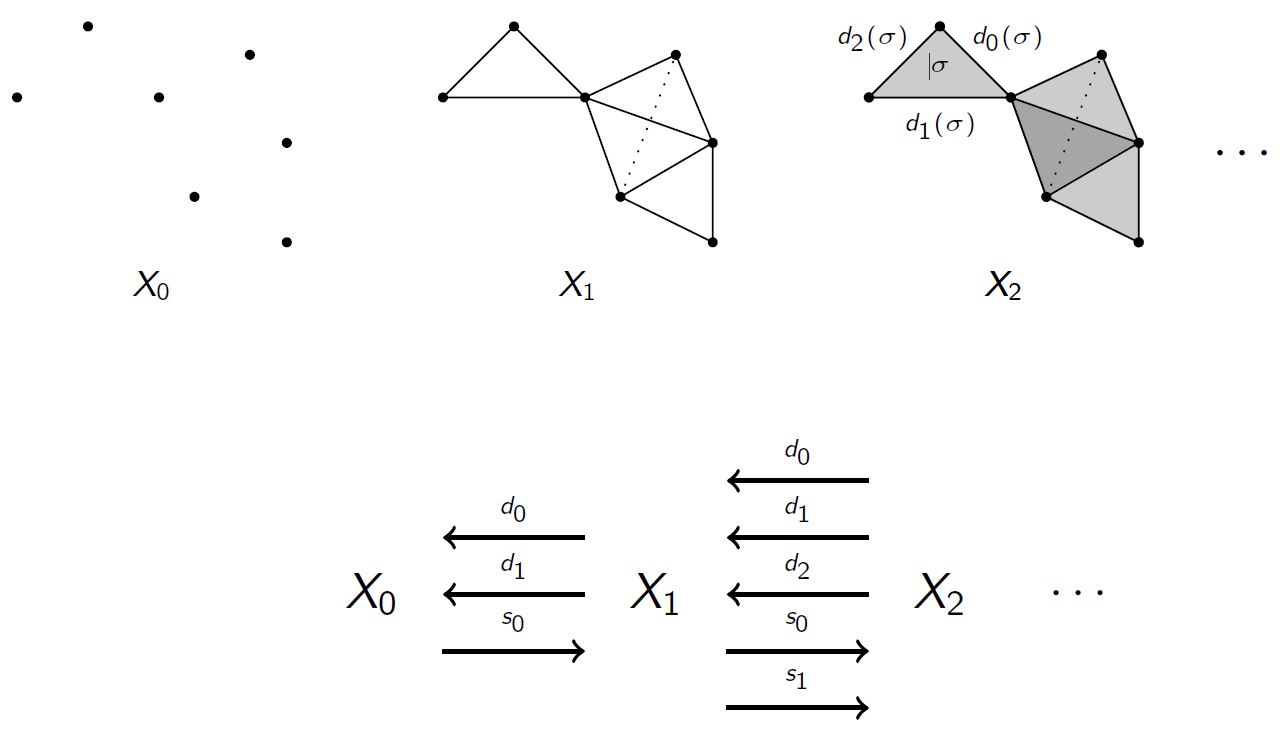
Example – The canonical cylinder object
on the 2-simplex look as follows
graphics grabbed from Friedman 08, p. 33
∞-groupoids
A simplicial set is called a Kan complex if
-
its -simplices may be composed
-
each has an inverse under composition, up to -simplices
These are the good models for simplicial homotopy types.
Example – a discrete group , is a Kan complex with
-
a single 0-simplex
-
1-simplices the group elements
-
2-simplices their product
-
3-simplices their associativity
An adjunction between model categories
is called a Quillen adjunction
if, very roughly (see here)
-
the left adjoint preserves cylinder objects;
-
the right adjoint preserves path space objects.
This induces an adjunction of derived functors on homotopy categories
This is a Quillen equivalence if the derived adjunction is an equivalence of categories
Example
simplicial and topological homotopy theory are Quillen equivalent
via forming
(Quillen 67)
Hence both represent
the homotopy theory of ∞-groupoids.
Remarkable richness of homotopy theory:
For a pointed object and a morphism
define the homotopy fiber of over by:
-
is in the fiber, up to homotopy:
-
is universal with this property.
Then short exact sequences become long homotopy fiber sequences:
example:
higher central extensions of super L-∞ algebras
are homotopy fibers of the corresponding cocycles :
4) Higher super geometry
So far we have established two ingredients:
-
realization of the Pauli exclusion principle:
affine superspaces formally dual to dgc-superalgebras,
such as super Cartesian spaces, super L-∞ algebroids
-
realization of the gauge principle:
homotopy theory,
notably of geometrically discrete ∞-groupoids (Kan complexes)
Now to combine this to
supergeometric ∞-groupoids (“∞-stacks”) in higher supergeometry.
Consider any category of affine spaces as above
We may bootstrap a notion of generalized spaces:
Geometry as seen by classical sigma-models:
To determine a generalized target space …
…consider for each brane worldvolume
the collection of sigma-model fields
Minimum consistency conditions.
-
For every , there should be a simplicial set
“of sigma-model fields into and their gauge-of-gauge equivalences”
(see also the talk by E. Sharpe at the meeting)
quotation marks because is yet to exist, will be removed in a moment
-
For every morphism in there should be a function
“precomposition of sigma-model fields with ”:
-
Compatibility with composition of morphisms in .
In the language of category theory this is simply summarized by:
Classical sigma-models see generalized spaces
as functors of the form
also called simplicial presheaves on .
Hence the category of generalized spaces
should be a full subcategory of the functor category
also called the simplical presheaf topos over .
This is naturally a model category: the global model structure on simplicial presheaves:
key bootstrap theorem of functorial geometry says that
the wish becomes true; we may remove the quotation marks:
known as the Yoneda lemma.
Direct consequence is the key consistency result
hence a full subcategory embedding
called the Yoneda embedding.
Impose one more condition: locality.
If is covered
by patches
then a decent generalized space should satisfy:
If satisfies this locality condition
it is called an ∞-stack or (∞,1)-sheaf over .
There is a local model structure on simplicial presheaves
and a Quillen adjunction (“Bousfield localization”)
whose derived adjunction on homotopy categories
is the full subcategory inclusion on the ∞-stacks
This homotopy theory is called the
∞-stack ∞-topos over
or
(∞,1)-sheaf ∞-topos over

Now to get higher supergeometry
specify to SuperCartesianSpaces
So super geometric homotopy theory is
this subsumes a rich amount of particular geometries
discussed in the literature:

5) Higher super Lie theory
In particular we have a variety of notions of geometric symmetry groups
Lie groups smooth ∞-groups
Lie groupoids smooth ∞-groupoids
super Lie groups super smooth ∞-groups
these should be related to
the super L-∞ algebroids discussed above
by higher Lie theory
idea (due to Ševera 01,
see also Pavol Ševera‘s talk at the meeting):
generalize the path method of Lie integration:
For a Lie algebra
and its simply connected Lie group
observe that parallel transport
(after a choice of base point)
provides a bijection
Hence we recover via smooth homotopy theory as
to generalize this
recall the functor of super differential forms
Consider its enhancement to smooth differential forms on simplices:
where
-
is the standard k-simplex as a smooth manifold with boundaries and corners;
-
“vert” = vertical differential forms: all legs along the k-simplex;
-
“si” = forms with sitting instants: constant towards boundary of k-simplex
(Fiorenza-S.-Stasheff 12, Def. 4.2.1; see Braunack-Mayer 18, Def. 3.1.3)
higher super Lie integration via higher super path method
for a super L-∞ algebra
with Chevalley-Eilenberg algebra
Let
be given by the simplicial presheaf
(Fiorenza-S.-Stasheff 12)
example:
For a Lie algebra with simply connected Lie group , we recover
Theorem (Braunack-Mayer 18)
higher super Lie integration is part of a Quillen adjunction
hence induces a derived adjunction on homotopy categories:
Theorem (Braunack-Mayer 18)
higher super Lie integration restricts to the Sullivan de Rham adjunction
classical fact of rational homotopy theory:
the derived adjunction restricts to an equivalence of categories
(for more on this see D. Fiorenza‘s and V. Braunack-Mayer’s talks at the meeting)
This implies that
higher super Lie integration preserves homotopy fiber sequences
hence in particular higher central extensions
6) Emergence of M-theory
homotopy theory reveals rich inner structure of god-given objects
Already the homotopy integers – known as the sphere spectrum –
exhibit endless patterns, order and chaos:

(the 2-primary components of the first few stable homotopy groups of spheres)
The microscope of homotopy theory is the Postnikov-Whitehead tower
For example Postnikov-Whitehead tower of the orthogonal group:
where each rectangle is a homotopy fiber square.
Under higher Lie integration this corresponds to
tower of universal higher central extensions of L-∞ algebras
As the terminology indicates (string Lie 2-algebra, fivebrane Lie 6-algebra,…),
pure homotopy theory is beginning to see string theory-structure…
(Sati-S.-Stasheff 09, Fiorenza-S.-Stasheff 10, Sati 14)
To get to the bottom of this
apply this microscope to the superpoint
regarded as a super Lie algebra, hence as a higher superspace
Consider iteratively the
invariant universal higher central extensions,
at each stage invariant with respect to automorphisms modulo R-symmetries
Then the following brane bouquet is revealed…
(Fiorenza-Sati-S. 13, Huerta-S. 17, BraunackMayer-Sati-S. 18, Huerta-Sati-S. 18,
see the talks by H. Sati, V. Braunack-Mayer, D. Fiorenza, J. Huerta (here) at the meeting):

Hence in super homotopy theory
core structure of M-theory emerges
out of the superpoint.
Does the superpoint itself emerge by itself?
To see this, we invoke now a yet stronger microscope,
that of modal homotopy theory
(see also Modern Physics formalized in Modal Homotopy Type Theory)
A reflective subcategory is
a fully faithful functor with a left adjoint
A modal operator is the resulting endofunctor
which projects onto .
dually:
A coreflective subcategory
is a fully faithful functor with a right adjoint
A comodal operator is the resulting endofunctor
which projects onto .
similarly in homotopy theory:
A Quillen reflection
is Quillen adjunction whose derived adjunction is a reflective subcategory
etc.
example: the homotopy localization at an object ,
is the reflective subcategory of coefficients
representing -homotopy invariant cohomology
denote the corresponding modal operator by
an adjoint modality
is an adjunction (duality) between
a modal operator and a comodal operator
or
this expresses two dual and opposite subcategories
for example
with
is an adjoint modality,
expressing the dual opposition between even and odd numbers.
preorder on modal operators
by inclusion of the subcategories which they project onto
everything happens in between:
Given a progression of adjoint modalities
we say it provides
sublation of
if in addition
-
denoted
or
-
denoted
an adjunction of adjunctions,
hence a duality of dualities
is
hence is an adjoint triple
Proposition
We have a progression of adjoint modalities on SuperSpaces as follows:
In this way
the superpoint
emerges from nothing
by a progression of dual oppositions, their dualities and their sublation.
For details see the lecture notes